Профильная - тренировочные задания

Найдите наименьший корень уравнения $$sqrt{x^2-4x+4}=2$$

Период свободных колебаний (в с) пружинного маятника определяется по формуле $$T=2pisqrt{frac mk}$$, где m — масса груза (в кг), k — жесткость пружины (в Н/м), $$pi=3$$. Груз какой массы (в кг) нужно закрепить на пружине жёсткостью 400 Н/м, чтобы период колебаний составил 0,9 с?

Найдите значение выражения $$5^{log_5left(x^2-6x+1right)}$$ при х = —2.

Найдите наибольшее значение функции $$f(x)=sinleft(x-frac{13pi}{12}right)-cos(x-frac{13pi}{12})$$ на отрезке $$left[fracpi3;frac{11pi}{12}right]$$

Найдите значение коэффициента k, если известно, что касательная к графику функции $$y=kcosx+(5+k);sinx$$ в точке $$x_0=-fracpi3$$ параллельна прямой y = x + 2

Найдите точку максимума функции $$y;=-x^3+3x^2+24x-18$$

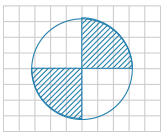
На клетчатой бумаге с размером клетки 1 см × 1 см изображена окружность. Вычислите площадь закрашенной фигуры в см².
В ответ укажите $$frac Spi$$.

В равнобедренном треугольнике ABC с основанием AC=$$6sqrt5$$ проведена высота BH=6 см. Найдите радиус описанной окружности треугольника ABC (в см).

Найдите корень уравнения $$x-sqrt x=2$$

Для проектировки закругления автотрассы координаты X поворотных точек находятся по формуле $$x_n=Rsin(ngamma)$$, где $$gamma$$ — угол поворота трассы в градусах, n — порядковый номер точки, R — радиус закругления автотрассы в метрах. Координата точки $$x_2=25sqrt3$$, а радиус закругления равен 50 м. Каков угол поворота трассы?
Ответ дайте в градусах.