Профильная - тренировочные задания
В правильной треугольной пирамиде высота равна 1 см. Найдите апофему пирамиды (в см), если радиус окружности, вписанной в основание, равен $$2\sqrt2$$.
На клетчатой бумаге с размером клетки 1 см × 1 см изображён квадрат, вписанный в окружность. Найдите площадь закрашенной фигуры (в см2). Число $$\pi$$ считайте равным 3.
Найдите наименьший корень уравнения $$2^{8-x^2}=\frac12$$
Для расчета сложных процентов по вкладу с учётом внутригодового начисления используется формула: $$F=P(1+\frac rm)^{nm}$$,
где P — исходная сумма (в руб.), r — годовая процентная ставка $$\left(r=\frac\%{100}\right)$$, n — количество лет, m — количество внутригодовых начислений.
В конце первого года на счету было 165 375 руб. Определите исходную сумму вклада (в руб.), если процентная ставка 10 % и внутригодовых начислений было 2.
Велогонщику предстоит преодолеть несколько участков пути по 30 км каждый. Известно, что на каждом следующем участке пути скорость гонщика уменьшается на одно и то же значение по сравнению с предыдущими 30 км. Определите, сколько времени (в часах) займет у велосипедиста преодоление шестого участка, если известно, что первый участок он проехал за 1 час 12 минут, а скорость на 4 участке составляла 22 км/ч.
Из города А в город В в одно и то же время выехали два автомобиля. Расстояние между городами 350 км. Второй автомобиль проехал с постоянной скоростью и без остановок весь путь. Первый автомобиль проехал первую половину пути, затем сделал остановку на 1 час, после чего продолжил путь с прежней скоростью. В итоге первый автомобиль прибыл в город В на 3 часа позже, чем второй. Найдите скорость второго автомобиля, если известно, что она больше скорости первого на 20 км/ч. Ответ дайте в км/ч.
Фермер Молочный с 2005 года по 2016 год занимался животноводством. На диаграмме показано количество коров и телят у этого фермера за всё время занятия этим бизнесом. По горизонтали указаны годы, а по вертикали — количество коров и телят в каждый год.
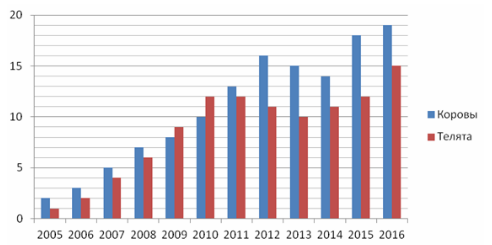
Определите по диаграмме, сколько лет количество телят у фермера превышало количество коров.
Площадь поверхности сферы равна 48π см2 . Найдите сторону куба (в см), вписанного в данную сферу.
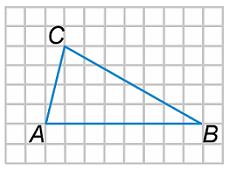
Каждая клетка имеет размер 1х1. Найдите длину отрезка АВ.
На клетчатой бумаге с размером клетки 1 см × 1 см изображён треугольник. Найдите длину медианы, проведенной из вершины C. Ответ дайте в см.
