Вариант 12 ЕГЭ по математике - тренировочные задания

Найдите значение выражения $$\frac{\sqrt3-\sqrt3sin^2(420^\circ)}{cos(150^\circ)}$$

Решите уравнение $$\sqrt{\frac2{6x+8}}=\frac1x$$. Если корней несколько, укажите бо́льший из них.

В городе c населением 720 000 человек 70 % населения не работает в бюджетной сфере. У 60 % бюджетников заработная плата ниже 15 тыс. рублей. Найдите количество бюджетников, заработная плата которых выше 15 тыс. рублей.

Все тела во Вселенной взаимодействуют между собой с силами, величину которых можно определить по закону всемирного тяготения $$F=G\frac{m_1m_2}{R^2}$$, где G = 6,67 • 10^-11м³ • с^-2 • кг^-1 — гравитационная постоянная, m₁ — масса второго тела в килограммах, R — расстояние между телами в метрах. Найдите расстояние между телами (в м), если масса первого тела равна 1000 кг, масса второго тела равна 5000 кг, а сила их взаимодействия 8,3375 • 10^-5 H.

Вероятность солнечного дня в октябре равняется 0,35. Найдите вероятность того, что 4 октября будет облачно, а 5 октября будет солнечная погода.

На диаграмме изображены два графика: уровень рождаемости и уровень смертности в городе N в период с 2000 по 2010 годы. По горизонтали отмечены года, по вертикали — уровень рождаемости и уровень смертности. Точки для наглядности соединены линиями. Прирост населения считается следующим образом: из уровня рождаемости вычитается уровень смертности.

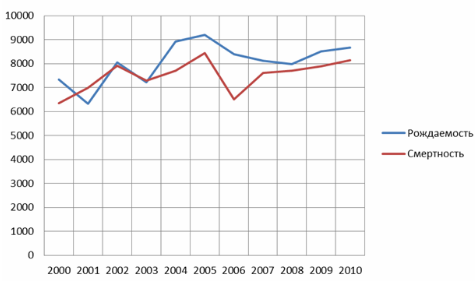
По графику определите, в каком году прирост населения был наибольшим.

В равнобедренную трапецию с основаниями AB и CD вписана окружность. Найдите бо́льшее основание трапеции (в см), если AB=6 см, BC=8 см.

Из пункта A стартовали два раллиста, первый из которых прибыл в пункт B на полчаса раньше второго. Если бы второй гонщик двигался на 20 км/ч медленнее, то первый обогнал бы его на час. Найдите скорость второго гонщика (в км/ч), если расстояние между пунктами A и B равно 300 км.

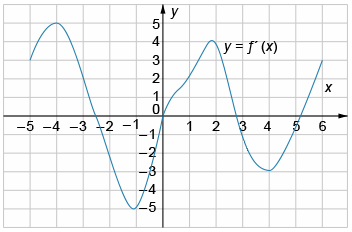
На рисунке представлен график производной функции y=f(x) на интервале [−5; 6]. Найдите количество точек экстремума функции y=f(x) на промежутке (−3; 4).

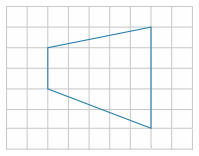
Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.