Найдите наибольшее значение функции $$f(x)=sinx+frac{sin2x}2$$ на промежутке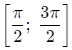

$$f'(x)=cosleft(xright)+cosleft(2xright)=cosleft(xright)+cos^2left(xright)-sin^2left(xright)=cosleft(xright)+cos^2left(xright)+cos^2left(xright)-1=2cos^2left(xright)+cosleft(xright)-1$$

На заданном промежутке производная - отрицательная, значит функция монотонно убывает.

f($$fracpi2$$)=1 - наибольшее значение функции на заданном промежутке

f($$frac{3pi}2$$)=-1