На олимпиаде по математике даются 8 задач, каждая из которых оценивается по семибалльной шкале. Первое место получает тот, кто в сумме набрал больше всех баллов и получил как минимум 1 балл не менее,
На олимпиаде по математике даются 8 задач, каждая из которых оценивается по семибалльной шкале. Первое место получает тот, кто в сумме набрал больше всех баллов и получил как минимум 1 балл не менее, чем в шести задачах. Номера участников и набранные ими баллы представлены в таблице.
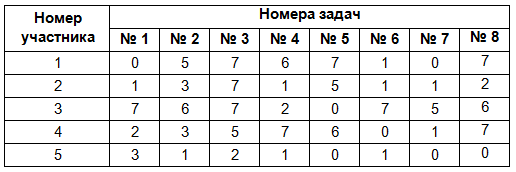
Пользуясь таблицей, определите, сколько баллов набрал победитель.
Тот у кого более 2х нулей за задачи первое место получить уже не сможет. У 5го участника 3 нуля, так что посчитаем и сравним балы остальных 4х.
0+5+7+6+7+1+0+7=33
1+3+7+1+5+1+1+2=21
7+6+7+2+0+7+5+6=40 — это наш победитель
2+3+5+7+6+0+1+7=
40
