В эксперименте была поставлена задача определить ускорение бруска при скольжении вниз по наклонной плоскости длиной l (1). Сначала была получена формула для расчёта ускорения: $$a=frac{mg;sina
В эксперименте была поставлена задача определить ускорение бруска при скольжении вниз по наклонной плоскости длиной l (1).
Сначала была получена формула для расчёта ускорения:
$$a=frac{mg;sinalpha-mu mg;cosalpha}m=g(sinalpha-mu;cosalpha)$$
Затем был исполнен подробный рисунок с размерами наклонной плоскости а (2) и положением векторов сил и их проекций.
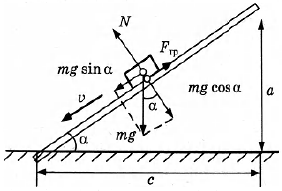
Значение коэффициента трения μ (3) дерева по дереву экспериментатор взял из справочных данных. Сила трения Fтр (4) и сила тяжести mg (5) были измерены динамометром. Какими из помеченных цифрами величин достаточно воспользоваться, чтобы определить ускорение бруска?
Ответ: ____
Из условия видно что для того что бы решить задачу необходимо подставить в конечную формулу некоторые значения, а именно коэффициент трения $$mathrmmu$$, и косинус и синус угла $$alpha$$, для нахождения косинуса необходимо знать противолежащий катет и гипотенузу, а для синуса прилежащий и гипотенузу.
Зная 2 стороны в прямоугольном треугольнике не сложно найти третью по теореме Пифагора.
Значит необходимые и достаточные данные для решения задачи будут 1 2 и 3
123
